So, last week I solved an easy problem but it was an interesting one! Uses of it applied in the world of frontend programming, and knowing how to solve such problems is quite valuable down the road when doing validation and processing-related tasks.

Challenge statement

The challenge statement is: given an array of error objects, we need to flatten its property constraints and transform them to a string array with the accurate property depth.

In a nutshell, this is what we need to solve: -

const errors = [
  {
    property: "applicant",
    children: [
      {
        property: "identity",
        children: [
          {
            property: "passport",
            children: [
              {
                property: "expiryDate",
                children: [],
                constraints: {
                  expired: "expiryDate is no longer valid",
                  format: "expiryDate must be in the format DD/MM/YYYY"
                }
              },
              {
                property: "issuedDate",
                constraints: {
                  validity: "issuedDate must be greater than 01/01/2018",
                  format: "issuedDate must be in the format DD/MM/YYYY"
                }
              }
            ],
            constraints: {
              prefix: "passport number should start with a capital letter",
              maxChars: "passport should be a string no more than 12 characters"
            }
          },
          {
            property: "nationalIdentityCard",
            children: [],
            constraints: {
              isNumber: "nationalIdentityCard must be a 12 digit number"
            }
          }
        ]
      },
      {
        property: "age",
        constraints: {
          isNumber: "age must be a number larger than 18"
        }
      }
    ]
  },
  {
    property: "studentId",
    constraints: {
      isNumber:
        "studentId must be a number conforming to the specified constraints"
    }
  }
];

And transform the above errors to this: -

const transformedErrors = {
  "applicant.identity.passport.expiryDate": [
    "expiryDate is no longer valid",
    "expiryDate must be in the format DD/MM/YYYY"
  ],
  "applicant.identity.passport.issuedDate": [
    "issuedDate must be greater than 01/01/2018",
    "issuedDate must be in the format DD/MM/YYYY"
  ],
  "applicant.identity.passport": [
    "passport number should start with a capital letter",
    "passport should be a string no more than 12 characters"
  ],
  "applicant.identity.nationalIdentityCard": [
    "nationalIdentityCard must be a 12 digit number"
  ],
  "applicant.age": ["age must be a number larger than 18"],
  studentId: [
    "studentId must be a number conforming to the specified constraints"
  ]
};

A part of the challenge is to solve this using JavaScript. But we will utilize TypeScript to write our solution in the upcoming sections.

Elaboration

Well, it seems like a piece of cake, right? We can solve this quickly if we take a minute or two to understand its schematic structure correctly.

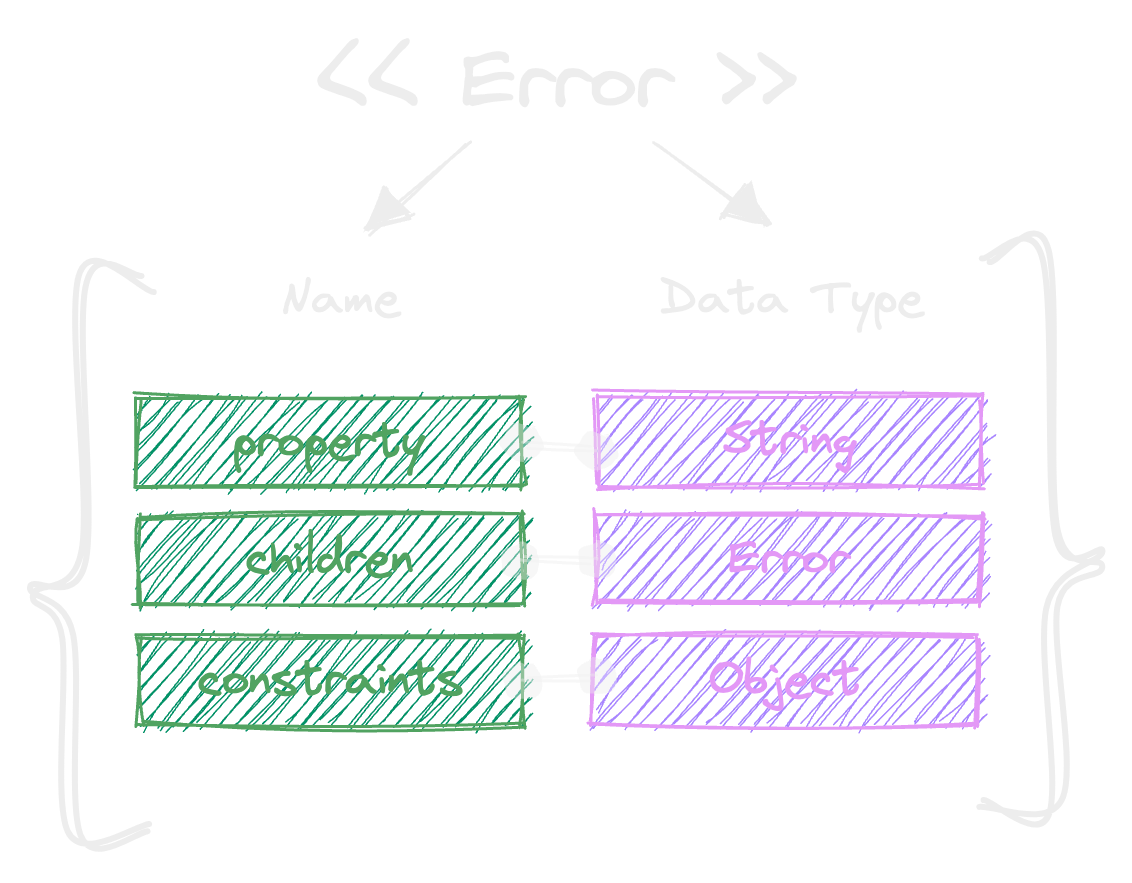
And if we transform this into more approachable static sorts we would get the following types.

export type Constraints = {
  [key: string]: string;
};

export type Error = {
  property: string;
  children?: Error[];
  constraints?: Constraints;
};

export type Result = {
  [key: string]: string[];
};

Looking at the challenge statement example, we can see that not all Error objects contain the children property. Hence, we should understand that one or more depths will have zero constraints or children to flatten. Therefore, we can safely ignore such results from the transformed object.

We can break down the problem into multiple steps to further simplify our approach. From my interpretation, we have four main tasks to focus on; and those are: -

1. Extract the string values from the constraints object.
2. Concatenate the children’s property path along with depth.
3. Go through all the children errors.
4. Assign constraints to the path (if there are any).

So how can we crack this?

Solution

We have to use either an iterative or a recursive to solve this problem. First, we can directly jump in and focus on the 1^st step, extracting the values from the constraints object.

We can write a helper function that accepts a given constraints object and return its extracted strings.

const extractConstraints = (constraints: Constraints): string[] => {
  const strings = [];
  for (const [, value] of Object.entries(constraints)) {
    strings.push(value);
  }
  return strings;
};

Then we can focus on 2^nd step, concatenating the children’s property path along with depth.

const concatProperty = (parent: Error, child: Error) => {
  return Object.assign(child, {
    property: `${parent.property}.${child.property}`
  });
};

Then the 3^rd step, going through all the children errors. But before that, we need another top-level helper function to compose the algorithm.

I will name it transformError with two parameters in place. The first parameter is an individual error itself and the second is our transformation result object.

const transformError = (error: Error, result: Result) => { };

Then we should first see whether there are any children available in this error object because remember, it can be optional.

const transformError = (error: Error, result: Result) => {
  // Then check whether this error has children.
  if (error.children) {
      // Do something
  }
}

So now, if the error has children then we should go through its children to recursively extract all their constraints.

const transformError = (error: Error, result: Result) => {
  // Then check whether this error has children.
  if (error.children) {
    for (const child of error.children) {
      transformError(concatProperty(error, child), result);
    }
  }
};

This is great! Now that we are only left with the 4^th step, and we can easily append the extractConstaints at last.

const transformError = (error: Error, result: Result) => {
  // Then check whether this error has children.
  if (error.children) {
    for (const child of error.children) {
      transformError(concatProperty(error, child), result);
    }
  }

  let flatConstraints: string[] = [];

  // if the error has constraints, then extract them.
  if (error.constraints) {
    flatConstraints = extractConstraints(error.constraints);
  }
  // if and only if there's constraints, assign them.
  if (flatConstraints.length) {
    result[error.property] = flatConstraints;
  }
};

We consolidate the last three points into a single function called transformError because they are recurring tasks. By doing this, we should be able to iterate through all the errors and recurse all the children accurately.

And finally, putting it all together, we get this: -

export type Constraints = {
  [key: string]: string;
};

export type Error = {
  property: string;
  children?: Error[];
  constraints?: Constraints;
};

export type Result = {
  [key: string]: string[];
};

/**
 * Given the constraints object, it returns an array of strings
 * that contains the values of that object.
 * @param {Constraints} constraints
 */
const extractConstraints = (constraints: Constraints): string[] => {
  const strings = [];
  for (const [, value] of Object.entries(constraints)) {
    strings.push(value);
  }
  return strings;
};

/**
 * Concatenates child error property with the parent property.
 * @param {Error} parent
 * @param {Error} child
 */
const concatProperty = (parent: Error, child: Error) => {
  return Object.assign(child, {
    property: `${parent.property}.${child.property}`
  });
};

/**
 * Flattens a given error. If there's children and it
 * recurse through the children depth.
 * @param {Error} error
 * @param {Result} result
 */
const transformError = (error: Error, result: Result) => {
  // Then check whether this error has children.
  if (error.children) {
    for (const child of error.children) {
      transformError(concatProperty(error, child), result);
    }
  }

  // initializing an empty to evaluate the
  // length of flattened constraints.
  let flatConstraints: string[] = [];

  // if the error has constraints, then extract them.
  if (error.constraints) {
    flatConstraints = extractConstraints(error.constraints);
  }
  // if and only if there's constraints, assign them.
  if (flatConstraints.length) {
    result[error.property] = flatConstraints;
  }
};

const formatErrors = (input: object[]): Result => {
  const result: Result = {};
  for (const error of input) {
    transformError(error as Error, result);
  }
  return result;
};

See? formatErrors function is the starting point of our algorithm. We iterate through all the errors we get as the input and calls the transformError with the result instance to hold the flattened records.

Time complexity

The analysis of the time complexities of this algorithm is quite straightforward. Since we use a recursive approach we can directly apply the master theorem to get the asymptotic estimates.

Where $n$ is the length of errors and $x$ is the depth of children in each error object.

Well, that’s it folks! Thanks for reading.